几道题目记录

主要记录一下几道题目，不记得哪个CTF比赛的题了。

easy_RAS

文件内容包括：

n:0x9371c61a2b760109781f229d43c6f05b58de65aa2a674ff92334cb5219132448d72c1293c145eb6f35e58791669f2d8d3b6ce506f4b3543beb947cf119f463a00bd33a33c4d566c4fd3f4c73c697fa5f3bf65976284b9cc96ec817241385d480003cdda9649fa0995b013e66f583c9a9710f7e18396fbf461cb31720f94a0f79L
e:0x3
encrypt(m):0x5f4e03f28702208b215f39f1c8598b77074bfa238dfb9ce424af7cc8a61f7ea48ffbbd5a5e1a10f686c3f240e85d011f6c8b968d1d607b2e1d5a78ad6947b7d3ec8f33ad32489befab601fe745164e4ff4aed7630da89af7f902f6a1bf7266c9c95b29f2c69c33b93a709f282d43b10c61b1a1fe76f5fee970780d7512389fd1L
encrypt(m+1):0x5f4e03f28702208b215f39f1c8598b77074bfa238dfb9ce424af7cc8a61f7ea48ffc5c26b0c12bcff9f697f274f59f0e55a147768332fc1f1bac5bbc8f9bb508104f232bdd20091d26adc52e36feda4a156eae7dce4650f83fabc828fdcfb01d25efb98db8b94811ca855a6aa77caff991e7b986db844ff7a140218449aaa7e8L

考的点是RSA算法，已知n、e、m和m+1, 计算明文。已知
$$
(m ^ e) = k_1n+encrypt(m)
$$
和
$$
(m+1)^e =k_2n+encrypt(m+1)
$$
联立两个方程，相减，可以得出，其中，两个k可以视为相等，因为两个加密的数据相近：
$$
(m+1)^3-m3=(encrypt(m+1)-encrypt(m))
$$
化简得：
$$
3m(m+1)=(encrypt(m+1)-encrypt(m))-1
$$
可以将m+1视为m，粗略计算出m的范围，然后通过一步步爆破每个字符来计算密码，解密脚本如下：

N =  0x9371c61a2b760109781f229d43c6f05b58de65aa2a674ff92334cb5219132448d72c1293c145eb6f35e58791669f2d8d3b6ce506f4b3543beb947cf119f463a00bd33a33c4d566c4fd3f4c73c697fa5f3bf65976284b9cc96ec817241385d480003cdda9649fa0995b013e66f583c9a9710f7e18396fbf461cb31720f94a0f79
c1 = 0x5f4e03f28702208b215f39f1c8598b77074bfa238dfb9ce424af7cc8a61f7ea48ffbbd5a5e1a10f686c3f240e85d011f6c8b968d1d607b2e1d5a78ad6947b7d3ec8f33ad32489befab601fe745164e4ff4aed7630da89af7f902f6a1bf7266c9c95b29f2c69c33b93a709f282d43b10c61b1a1fe76f5fee970780d7512389fd1
c2 = 0x5f4e03f28702208b215f39f1c8598b77074bfa238dfb9ce424af7cc8a61f7ea48ffc5c26b0c12bcff9f697f274f59f0e55a147768332fc1f1bac5bbc8f9bb508104f232bdd20091d26adc52e36feda4a156eae7dce4650f83fabc828fdcfb01d25efb98db8b94811ca855a6aa77caff991e7b986db844ff7a140218449aaa7e8
e = 3

c3 = c2-c1-1

count = 0

d1 = int(c3/3)
p = 0x746865206b657920000000000000000000000000000000000000000000000000000000000000000000000000000000
q = p+1
ss = 0x10000000000000000000000000000000000000000000000000000000000000000000000000000
sd = 0x200000000000000000000000000000000000000000000000000000000000000000000000000000
tmp_p = p
while True:
    tmp_p=tmp_p+sd
    count = 0x20
    while True:
        tmp_p+=ss
        count +=1
        if (tmp_p*(tmp_p+1))>d1:
            break
        if count > 0x7e:
            break
    tmp_p = tmp_p-ss
    sd = sd>>8
    ss = ss>>8
    if sd==0:
        break
print hex(tmp_p)[2:-1].decode('hex')

计算出解压密码为：the key is :everything_is_easy_in_this_question

解开压缩包，发现是一个一次一密的密文：

280316470206017f5f163a3460100b111b2c254e103715600f13,
091b0f471d05153811122c70340c0111053a394e0b39500f0a18,
4638080a1e49243e55531a3e23161d411a362e4044111f374409,
0e0d15470206017f59122935601405421d3a244e10371560140f,
031a08080e1a540d62327f242517101d4e2b2807177f13280511,
0a090f001e491d2c111d3024601405431a36231b083e022c1d,
16000406080c543854077f24280144451c2a254e093a0333051a,
02050701120a01334553393f32441d5e1b716027107f19334417,
131f15470800192f5d167f352e0716481e2b29010a7139600c12,
1609411e141c543c501d7f232f0812544e2b2807177f00320b1f,
0a090c470a1c1d3c5a1f2670210a0011093a344e103715600712,
141e04040f49153142043a22601711520d3a331d0826

flag用于重复加密，可以利用语法和空格来计算明文：

s = [0x280316470206017f5f163a3460100b111b2c254e103715600f13,
0x091b0f471d05153811122c70340c0111053a394e0b39500f0a18,
0x4638080a1e49243e55531a3e23161d411a362e4044111f374409,
0x0e0d15470206017f59122935601405421d3a244e10371560140f,
0x031a08080e1a540d62327f242517101d4e2b2807177f13280511,
0x0a090f001e491d2c111d3024601405431a36231b083e022c1d,
0x16000406080c543854077f24280144451c2a254e093a0333051a,
0x02050701120a01334553393f32441d5e1b716027107f19334417,
0x131f15470800192f5d167f352e0716481e2b29010a7139600c12,
0x1609411e141c543c501d7f232f0812544e2b2807177f00320b1f,
0x0a090c470a1c1d3c5a1f2670210a0011093a344e103715600712,
0x141e04040f49153142043a22601711520d3a331d0826]

flag = 0x666c61677b69745f31735f50406464316e5f406e645f7040647d

a = 0
print hex(flag)[2:-1].decode('hex')
for i in s:
    a+=1
    print hex(i)
    print hex(flag)
    print hex(i^flag)[2:-1].decode('hex')

flag:flag{it_1s_P@dd1n_@nd_p@d}

ezmath

ezmath是国赛的一道逆向题，这道题的考点是一个数学题，但是题目存在一定的问题，输入的值就算是正确的flag也无法通过。

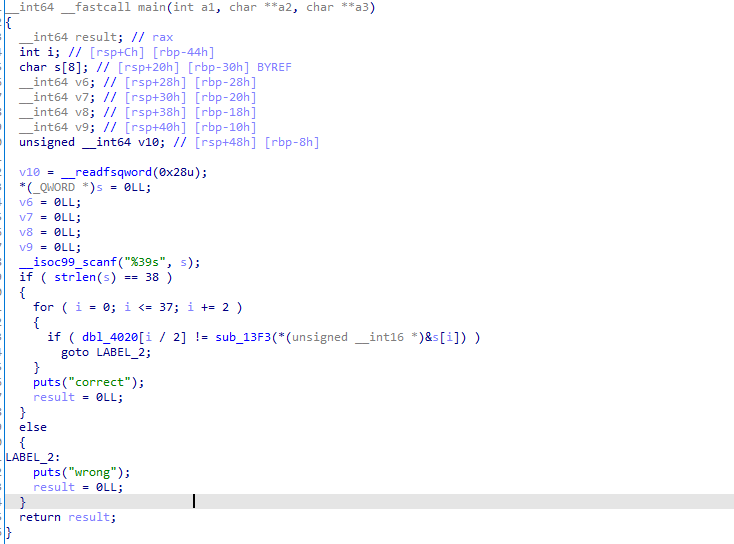
查看主函数代码逻辑：

其中，sub_13F3函数可以视为一个加密函数，加密的结果与dbl_4020处的值进行比较：

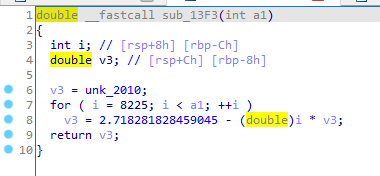
sub_13F3函数：

这是一个简单的循环逻辑。

函数总的逻辑就是将输入的flag两个字符转为一个数值，例如’fl’=>0x666c

循环次数是从2021一直到转换到这个数值，存在的问题是，这个循环次数太多，导致最后的生成的数据无限大，所以常规的分析无法实现。

同对数据随意进行操作，我发现，可以让2.718281828459045除以结果，得到值非常像flag，所以：

v3 = 0.0004829108052495089
table = [0.00009794904266317233, 0.00010270456917442, 0.00009194256152777895,
 0.0001090322021913372, 0.0001112636336217534, 0.0001007442677411854,
 0.0001112636336217534, 0.0001047063607908828, 0.0001112818534005219,
 0.0001046861985862495, 0.0001112818534005219, 0.000108992856167966,
 0.0001112636336217534, 0.0001090234561758122, 0.0001113183108652088,
 0.0001006882924839248, 0.0001112590796092291, 0.0001089841164633298,
 0.00008468431512187874]
tt = 2.718281828459045
# for i in table:
#     print(tt)
flag = ''
for i in table:
    a = chr(int(hex(int(tt/i)-1)[2:4],16))
    b = chr(int(hex(int(tt/i)-1)[4:6],16))
    flag+=b
    flag+=a
print(flag)

flag:flag{saam_dim_gei_lei_jam_caa_sin_laa}

某个不记得出处的密码题

题目：

def get_prime(bits):
    x = 1
    while gmpy2.is_prime(x) == False:
        random.seed(round(time.time(),5))
        x = random.getrandbits(bits)
    return x

hint = ""
a1 = time.time()
flag = "flag{***************}"
p = get_prime(2048)
q = get_prime(2048)
n = p * q
e = 65537
m = bytes_to_long(flag.encode())
assert n > m
c = pow(m,e,n)
print(n)
print(c)
hint+=str(time.localtime())
hint+=str(time.time()-a1)

m2 = bytes_to_long(hint.encode())
e2 = 196611
p2 = getPrime(1024)
q2 = gmpy2.next_prime(p2)
n2 = p2*q2
assert n2 > m2
c2 = pow(m2,e2,n2)
print(n2)
print(c2)
c2=2468578221703379861458008098241051507850837382948845085288946175636556753744182763176189585173648323464054032011039944322939163396161712722541432975739789351064988098201326803586126788175259878398963744821667593495161587855894677387881240566285601934559118064797092685909593247713834262369686831071897653756217369182373679039639016628932948775518889507209432291038498366540263588850133348471811624348709494110881127292350302658720685976197632586315945770832849119141593343924518836983738868912332048462058640564551286493338707636203013048694776131295632886983835291684044170004544049944003732133038154121113518892438
n2=15155267112260254814859334094046172735826002259080171081726998162357946701645037659523881592272031544049749021927125983252197909993392636398184049160807707719999605547760868696059871234441249045293267592302009677249269002811886149589869652213333369608947939768457152200437978105250737118847430275142343554191304134468404921824671763164876924921101985937224297479095246132228051655664880892772136476378294042631659251586654877292836243536438334288184387617801131434535466414123998495813296765847561162680781100446656391077184870802746066619879552452560641945080540683058930700833439189784657690146144976738557801495769
n1=449389319572014470973230701130712522617269811294117721031111991008431585050360094769229957883125144692171901233101564003762866045169460601700254891441878998743810037070537170855056466702105713343963726437141651081516150688905082129849562489646846756872586122801890652177495174154676725874072596207108180178755008058522945203093993733331873167443162263746938403044201113440457668163574342481361454421154163291201432319013385234751292922268166299917246608164679144459355173725895117315662317330324505156929077922670671914823996700321766811999551043586214703010131467697982137884162143358399786007967117340789211505834848813471803797101083738140019127129356248286854522464787917597152171952002118368747491099723673529923018951195522714900400225757160886780159504182902140132857743474716967975019342128486236748643365288547828026395873270777532526144687248477070253203339428149026199554962987646174586568177797380361174318868448467648171416588868990979461995030684403161898497550408697577695094783000808003197203603068043364687265824456069673330314452567416143754983137647607219859034406220590219587869898727679465514015732749105798134650890143215022311113143974714405713221391896497966231925409438383535066648782822255201778169275281703
c1=401489532945377793610793684722119773544780301600066410745513430092738470870254235710677331662917458735216486816223654944666672512914069274195244871184555059503843032370247894353363929996813688885280857203101709839776411016868985545599944237897372546401710041402579657231598311853522596463296090177664832759103736040102780428858301594805054838853076238331373482465072766841859415172741329175814259920949065993852870119473982972519779774470087935094963692097673607052443800723940091927016071427616754775915389245004208964143538205414854133746775614714447645057516665851780628694481268861808310238416724971673673850671343955386054575121362377868533055225219936712709474708031320743579595394353267596208729974198335174409673325772679039734706841988107519076516144633301371408301344929883397145523702189363308278963683356102257750758738297143036846718834812930796483716912661191147997005333798193659914573185697664706530774799114804036170190966523509331071964600280701252628276934131586398546602582672541075820188456265586487083315680880306767899236884202195162421559689536613740573005749847000477194096162091015847386298782974979446476432285118251267512895876728805199744415821498028998351171848530921695254428997423725875714923331577073

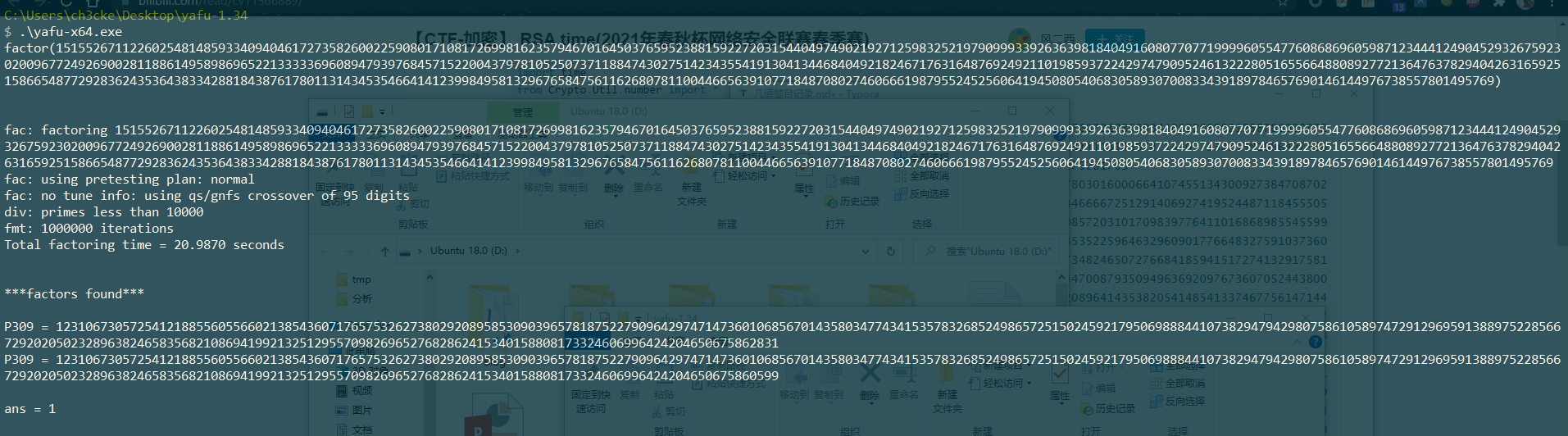
因为p和q十分接近，所以可以使用yafu直接分解：

可以解得：

p2 = 123106730572541218855605566021385436071765753262738029208958530903965781875227909642974714736010685670143580347743415357832685249865725150245921795069888441073829479429807586105897472912969591388975228566729202050232896382465835682108694199213251295570982696527682862415340158808173324606996424204650675860599
q2 = 123106730572541218855605566021385436071765753262738029208958530903965781875227909642974714736010685670143580347743415357832685249865725150245921795069888441073829479429807586105897472912969591388975228566729202050232896382465835682108694199213251295570982696527682862415340158808173324606996424204650675862831
e2 = 196611
phi = (p2-1)*(q2-1)
d2 = gmpy2.invert(e2, phi)
m2 = pow(c2, d2, n2)
print(hex(m2)[2:].decode('hex'))

time.struct_time(tm_year=2021, tm_mon=4, tm_mday=28, tm_hour=20, tm_min=42, tm_sec=6, tm_wday=2, tm_yday=118, tm_isdst=0)3.1603143215179443

爆破：

n1=449389319572014470973230701130712522617269811294117721031111991008431585050360094769229957883125144692171901233101564003762866045169460601700254891441878998743810037070537170855056466702105713343963726437141651081516150688905082129849562489646846756872586122801890652177495174154676725874072596207108180178755008058522945203093993733331873167443162263746938403044201113440457668163574342481361454421154163291201432319013385234751292922268166299917246608164679144459355173725895117315662317330324505156929077922670671914823996700321766811999551043586214703010131467697982137884162143358399786007967117340789211505834848813471803797101083738140019127129356248286854522464787917597152171952002118368747491099723673529923018951195522714900400225757160886780159504182902140132857743474716967975019342128486236748643365288547828026395873270777532526144687248477070253203339428149026199554962987646174586568177797380361174318868448467648171416588868990979461995030684403161898497550408697577695094783000808003197203603068043364687265824456069673330314452567416143754983137647607219859034406220590219587869898727679465514015732749105798134650890143215022311113143974714405713221391896497966231925409438383535066648782822255201778169275281703

def get_prime(bits,dd):
    x = 1
    while gmpy2.is_prime(x) == False:
        if dd== time_end:
            break
        # print (round(time.time(),5))
        random.seed(round(dd,5))
        x = random.getrandbits(bits)
        dd+=0.00001
    return x, dd
 
if __name__ == '__main__':
    while True:
        d, time_start = get_prime(2048, time_start)
        print (time_start)
        if n1%d==0:
            print(d)
            break

p = 15360610070658756452775981220974692269754488069112447574228228635172518259707134514408315074592577390698594736605248087796101036697451547100410265895327560411294149316110964728238874696235929203731881998113781125348646341501219405620572607850544026471698636266490132324671879327975938781232776798316450395970997145320000569958972563105862963186117576276208073997763946153235287770074359557092366500382435482039438236868834374950888321780977585512229188837801768702376220882499000782771015183089522410298091322352922782284547034389739802236095714242735319203659400058027730963273141420889040535277149816754727342652031
q = 29255955167459173822029202653748208731665372392075310136166091626575381119996561344943898926895111560376898745160876509298700464980231887621948926920057583752649963205840641291654838365453417505593997914971784293790085743184284527598476737057527689694922200354165364024522488494310943036055262843225458488560113074237945109027019763172911986120412620473828687488483196046813755180263850690491049425246819627692939001093191158687966930218499663030472933603946985975956492839271737062304560756111632672448716026348929763876173656518558040564823003900583478638946595821096363093296973637163241707021374227978181941716313

c1=401489532945377793610793684722119773544780301600066410745513430092738470870254235710677331662917458735216486816223654944666672512914069274195244871184555059503843032370247894353363929996813688885280857203101709839776411016868985545599944237897372546401710041402579657231598311853522596463296090177664832759103736040102780428858301594805054838853076238331373482465072766841859415172741329175814259920949065993852870119473982972519779774470087935094963692097673607052443800723940091927016071427616754775915389245004208964143538205414854133746775614714447645057516665851780628694481268861808310238416724971673673850671343955386054575121362377868533055225219936712709474708031320743579595394353267596208729974198335174409673325772679039734706841988107519076516144633301371408301344929883397145523702189363308278963683356102257750758738297143036846718834812930796483716912661191147997005333798193659914573185697664706530774799114804036170190966523509331071964600280701252628276934131586398546602582672541075820188456265586487083315680880306767899236884202195162421559689536613740573005749847000477194096162091015847386298782974979446476432285118251267512895876728805199744415821498028998351171848530921695254428997423725875714923331577073
if __name__ == '__main__':
    p = 15360610070658756452775981220974692269754488069112447574228228635172518259707134514408315074592577390698594736605248087796101036697451547100410265895327560411294149316110964728238874696235929203731881998113781125348646341501219405620572607850544026471698636266490132324671879327975938781232776798316450395970997145320000569958972563105862963186117576276208073997763946153235287770074359557092366500382435482039438236868834374950888321780977585512229188837801768702376220882499000782771015183089522410298091322352922782284547034389739802236095714242735319203659400058027730963273141420889040535277149816754727342652031
    q = 29255955167459173822029202653748208731665372392075310136166091626575381119996561344943898926895111560376898745160876509298700464980231887621948926920057583752649963205840641291654838365453417505593997914971784293790085743184284527598476737057527689694922200354165364024522488494310943036055262843225458488560113074237945109027019763172911986120412620473828687488483196046813755180263850690491049425246819627692939001093191158687966930218499663030472933603946985975956492839271737062304560756111632672448716026348929763876173656518558040564823003900583478638946595821096363093296973637163241707021374227978181941716313
    phi1 = (p-1)*(q-1)
    d1 = gmpy2.invert(65537, phi1)
    m = pow(c1,d1,n1)
    print (hex(m)[2:])

flag:flag{8b583646-13e8-5ef7-97c6-34b636591265}